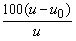Pareto Analysis

Pareto Analysis: When faced with a range of issues, it is often difficult to know which to work on first. To resolve this problem, the most useful thing to do is to apply Pareto's rule. It can be described as the 80/20 rule applied to quality-control.  The 80/20 rule was originally formalized by Vilifredo Pareto, after studying the distribution of wealth.  He noticed that about 80% of wealth was held by about 20% of the population. Several years later, Joseph Juran applied the principle to quality-control, and Pareto Analysis was born. Pareto Analysis essentially states that 80% of quality problems in the end product or service are caused by 20% of the problems in the production or service processes. Once these problems are identified, the 20% that are causing 80% of the problems can be addressed and remedied, thus efficiently obtaining quality.

It can be used in a technical sense to try and improve a process by eliminating defects.  It can be used in a human resources to try and find the time wasters in different work environment.  It can be used in finding out what the biggest hurdle may be to achieving a goal.

Use of Pareto Analysis:
An example of where one might use a Pareto Analysis might be if you were running a restaurant. Approximately 20% of the menu items would account for 80% of the profit taken in by the restaurant.  By using a Pareto Analysis, the restaurateur would know which menu items to focus his business around. In the manufacturing of clothing if one monitores the returns of clothing with a Pareto Analysis, the manufacturer would be able to find the 20% of the root causes behind 80% of the returns.  A third example can be seen in the semiconductor industry. Again, a manufacturing process will be looked at but this time the Pareto Analysis will be used inline to determine defect causes during inspection.  Using a Pareto Analysis, engineering can decide which defects warrant the most attention, cut costs, and improve the end result.

 A Pareto chart has the following objectives: 

-  Separate the few major problems from the many possible problems so you can focus your improvement    efforts. 

-  Arrange data according to priority or importance.

- Determine which problems are most important using data, not perceptions. 

Benefits of Pareto Analysis

Pareto diagrams: 

- Solves efficiently a problem by the identification and the hierarchisation, according to their importance, of the main causes of the faults. 

- Sets the priorities for many practical applications. Some examples are: process improvement efforts for increased unit readiness, customer needs, suppliers, investment opportunities. 

- Shows where to focus efforts. 

- Allows better use of limited resources. 

A Pareto Diagram is a good tool to use when the process investigated produces data that are broken down into categories and you can count the number of times each category occurs. A Pareto diagram puts data in a hierarchical order, which allows the most significant problems to be corrected first. The Pareto analysis technique is used primarily to identify and evaluate nonconformities, although it can summarize all types of data. It is the perhaps the diagram most often used in management presentations.

The Pareto chart

A Pareto chart is a graphical representation that displays data in order of priority. It can be a powerful tool for identifying the relative importance of causes, most of which arise from only a few of the processes, hence the 80:20 rule. Pareto Analysis is used to focus problem solving activities, so that areas creating most of the issues and difficulties are addressed first.

How to Use It

In conducting a Pareto Analysis, the first phase is concerned with identifying possible causes of inferior quality.  This can be done through brainstorming, focus groups, surveys, or any other method appropriate to the given business.  The goal is to obtain actionable items that result in inferior quality.  For example, if I manufacture glass windows, and some of them must be returned due to glass chips and cracks, I may identify the following four possible causes of the glass inconsistencies (inferior quality): poor production process, mishandling at the factory, faulty packaging, and problems in transit.  Each of these items can be acted upon, and in our situation, we will assume they are truly possible causes of inferior quality.  Once the actionable items are identified, we can move on to phase two.

The second phase is comprised of picking an appropriate time period over which we would like to conduct our analysis and then conducting the assessment.  The goal here is to obtain a statistical sampling that is representative of the time period over which we are trying to improve quality.  Some quality-control measures may be intentionally applied to seasonal, biannual, or some other specified time period, depending on the business.  Some businesses may care about the quality and increased investment of obtaining that quality at certain times of the year, but not at others.  The objective is to make sure that the measured time period accurately represents the time period over which the quality-control measures will be enacted.  Once the time period is chosen, the quality problems are tallied under the causes of inferior quality that were identified in the first phase.  In our example, each time we received a return for the reason of ‘faulty packaging,’ we would add one to the tally for that cause.  Each time we incurred an inconsistency for the reason of ‘mishandling at the factory,’ we would add one to the tally for that cause.  This process would continue until our predefined time period had elapsed, after which we would subtotal the results and move on to the third phase.

Phase three is summarizing and graphing the results obtained in the previous phases.  After subtotaling the numbers for each of the causes of inferior quality, those numbers are summed to obtain the total number of defects.  Then, in order to acquire the percentage of each cause in relation to the total number of defects, each subtotaled number is divided by the total number of defects and multiplied by 100.  After these percentages are obtained, they can be graphed in a histogram, with the causes of poor quality listed on the x-axis, and the percentages of their occurrence listed on the y-axis.  The causes are listed from left to right, with the most often occurring cause listed on the furthest left, the next most often occurring cause listed next to it, and so on.  Finally, in order to make the histogram more easily interpretable, a cumulative line graph can be placed over the existing bars.  This histogram is called a Pareto Chart.  Now we are ready for phase four.

The fourth and final phase is concerned with interpreting and applying the graphed results.  The overlaid line graph helps us in this process, as it shows the percentage of the total defects that we dispose of as we perform the actionable items, from left to right.  This is where the 80/20 rule comes into play, as you will most often notice that about 80% of the defective products are caused by about 20% of the possible defect causes.  When actually implementing solutions, however, it is recommended that after the leftmost quality problem is dealt with, that another Pareto Analysis is conducted before moving on to the other identified quality problems.  The reason for this is that the percentages for each of the remaining quality problems may shift disproportionately as the production or service process is changed in implementing the quality-control measures on the initial quality problem.  This caution may not always be necessary, but should be realized by the person conducting the analysis.

Pareto Analysis in Excel

Pareto charts are often used in quality control to display most common reasons for failure, customer complaints or product defects.

The principle behind pareto charts is called as pareto principle or more commonly the 80-20 rule

1) Once we have the values for each cause, we can easily calculate cumulative percentages. We will also require a dummy series to display the “cutoff %” in the Pareto chart.

 

 2) Make a column chart using cause importance data i.e., the data values in column 2 and the fields in column 1.

 

3) Add the cumulative % to the Pareto Chart as a line.

 

4) Move the cumulative % line to secondary axis. 

 

5) Add the cut-off % to the pareto chart.

 

 Now, our basic pareto analysis in excel is ready.

Read more

Inaccuracies in Data

How and Where Mistakes Arise: The only way to avoid mistakes is, of course, to work carefully but a general knowledge about the nature of mistakes and how they arise helps us to work carefully. Most mistakes arise at the stage of copying from the original material to the worksheet or from one worksheet to another, transferring from the worksheet onto the calculating machine or vice versa, and reading from mathematical tables. It is a good idea in any computational program to cut down copying and transferring operations as much as possible. A person who computes should always do things neatly in the first instance and never indulge in the habit of doing “rough work” and then making a fair copy. Computational steps should be broken up into the minimum possible number of unit operations - operations that can be carried out on the calculating machine without having to write down any intermediate answer. Finally the work should be so arranged that it is not necessary to refer to mathematical tables every now and then. As far as possible, all references to such tables should be made together at the same time : this minimizes the possibility of referring to a wrong page and of making gross mistakes in reading similar numbers from the same table. In many mathematical tables, when the first few digits occur repeatedly, they are separated from the body of the table and put separately in a corner; a change in these leading digits in the middle of a row is indicated by a line or some other suitable symbol. We should be careful to read the leading digits correctly from such tables.

Classification of Mistakes: Mistakes in copying, transferring and reading fall into three broad classes: digit substitution, juxtaposition and repetition. One mistake is to substitute hurriedly one digit for another in a number, for instance, 0 for 6, 0 for 9, 1 for 7, 1 for 4, 3 for 8, or 7 for 9. The only remedy is to write the digits distinctly. Another mistake is to alter the arrangement of the digits in a number, to write 32 for 23 or 547 for 457. The third type of mistake occurs when the same number or digit occurs repeatedly. For instance, 12,225 may be copied as 1225 or in the series of numbers 71, 63, 64, 64, 64,  . one  or more of the 64’s may be forgotten. We should be especially careful to avoid these mistakes.

Precautions: Certain general precautions should be taken to avoid mistakes in computations. Whenever possible, we should make provision for checking the accuracy of computation. One way is to make use of mathematical identities and compute the same quantity by different methods. Computations should be properly laid out, in tabular form, with check columns whenever possible. Further before starting on the detailed computations a few extra minutes may be taken for computing mentally as rough answer. This serves a check on the final computation. To summarize, we may lay down the following five principles for avoiding mistakes in computation:

·         Write the digits distinctly.

·         Cut down copying and transferring operations.

·         Use tabular arrangement for computations.

·         Keep provision for checking.

·         Guess the answer beforehand.

A last word of warning may be helpful. If a mistake is made, it is almost impossible to locate and correct the mistake by going through the original computation, even if this is done a number of times. The best way out is to work the whole thing afresh, perhaps using a different computational layout altogether.

It is convenient at the start to make a distinction between different types of accuracies in computational work. A blunder is a gross inaccuracy arising through ignorance. A statistician who knows his theory rarely commits a blunder. But even when he knows the procedure in detail and use machines for computations, he sometimes makes mistakes. There is a third type of inaccuracy, which we shall call an error. This is different from the other two types in that it is usually impracticable and sometimes even impossible to avoid. In other words an error is an observation which is incorrect, perhaps because it was recorded wrongly in the first place or because it has been copied or typed incorrectly at some stage. An outlier is a ‘wild’ or extreme observation which does not appear to be consistent with the rest of the data. Outliers arise for a variety of reasons and can create severe problems. Errors and outliers are often confused. An error may or may not be an outlier, while an outlier may not be an error.

The search for errors and outliers is an important part of Initial Data Analysis. The terms data editing and data cleaning are used to denote procedures for detecting and correcting errors. Generally this is an iterative and ongoing process.

Some checks can be made ‘by hand’, but a computer can readily be programmed to make other routine checks and this should be done. The main checks are for credibility, consistency and completeness. Credibility checks include carrying out a range test on each variable. Here a credible range of possible values is pre specified for each variable and every observation is checked to ensure that it lies within the required range. These checks pick up gross outliers as well as impossible values. Bivariate and multivariate checks are also possible. A set of checks, called ‘if-then’ checks, can be made to assess credibility and consistency between variables.

Another simple, but useful, check is to get a printout of the data and examine it by eye. Although it may be impractical to check every digit visually, the human eye is very efficient at picking out suspect values in a data array provided they are printed in strict column formation in a suitably rounded form. When a suspect value has been detected, the analyst must decide what to do about it. It may be possible to go back to the original data records and use them to make any necessary corrections. In some cases, such as occasional computer malfunctions, correction may not be possible and an observation which is known to be an error may have to be treated as a missing observation.

Extreme observations which, while large, could still be correct, are more difficult to handle. The tests for deciding whether an outlier is significant provide little information as to whether an observation is actually an error. Rather external subject-matter considerations become paramount. It is essential to get advice from people in the field as to which suspect values are obviously silly or impossible, and which, while physically possible, are extremely unlikely and should be viewed with caution. Sometimes additional and further data may resolve the problem. It is sometimes sensible to remove an outlier, or treat it as a missing observation, but this outright rejection of an observation is rather drastic, particularly if there is evidence of a long tail in the distribution. Sometimes the outliers are the most interesting observations.

An alternative approach is to use robust methods of estimation which automatically downweight extreme observations. For example, one possibility for univariate data is to use Winsorization, in which an extreme observation is adjusted towards the overall mean, perhaps to the second  most extreme value (either large or small as appropriate). However, many analysts prefer a diagnostic approach which highlights unusual observations for further study. Whatsoever amendments are required to be made to the data, there needs to be a clear, and preferably simple, sequence of steps to make the required changes in data.

Missing observations arise for a variety of reasons. A respondent may forget to answer all the questions, an animal may be killed accidentally before a treatment has shown any effect, a scientist may forget to record all the necessary variables or a patient may drop out of a clinical trial etc. It is important to find out why an observation is missing. This is best done by asking ‘people in the field’. In particular, there is a world of difference between observations lost through random event, and situations where missing observations are created deliberately. Further the probability that an observation, y, is missing may depend on the value of y and/or on the values of explanatory variables. Only if the probability depends on neither then the observations are said to be missing completely at random. For multivariate data, it is sometimes possible to infer missing values from other variables, particularly if redundant variables are included (e.g. age can be inferred from date of birth).

Errors may arise from one or more of the following sources : (a) the mathematical formulation is only an idealized and very seldom an exact description of reality; (b) parameters occurring in mathematical formulae are almost always subject to errors of estimation; (c) many mathematical problems can only be solved by an infinite process, whereas all computations have to be terminated after a finite number of steps;  (d) because of the limited digit capacity of computing equipment, computations have to be carried with numbers rounded off conveniently. However, it is not necessary to try to avoid all errors, because usually the final answer need be correct only to a certain number of figures. The theory of calculations with approximate numbers will be subjected to the following errors:

Rounding Off: Because of the limited digit capacity of all computing equipments, computations are generally be carried out with numbers rounded off suitably. To round off a number to n digits, replace all digits to the right of the n-th digit by zeros. If the discarded number contributes less than half a unit in the n-th place, leave the n-th digit unaltered; if it is greater than half a unit, increase the n-th digit by unity; if it is exactly half a unit, leave the n-th digit unaltered when it is an even number and increase it by unity when it is an odd number. For example, the numbers 237.582, 46.85, 3.735 when rounded off to three digits would become 238, 46.8 and 3.74, respectively.

Significant Figures: In a rounded-off number, significant figures are the digits 1, 2,..., 9. Zero (0) is also a significant figure except when it is used to fix the decimal point or to fill the places of unknown or discarded digits. Thus in 0.002603, the number of significant figures is only four. Given a number like 58,100 we cannot say whether the zeros are significant figures or not; to be specific we should write it in the form 5.81 x 10⁴, 5.810 x 10⁴ or 5.8100 x 10⁴ to indicate respectively that the number of significant figures is three, four or five.

Error Involved in the Use of Approximate Numbers : If   u  is the true value of a number and u₀  an  approximation  to  it,  then  the  error  involved  is   E = u - u_{0 .} The relative error is e =   and the percentage error is p = 

Read more

Exploring of data

“Garbage in, garbage out“ is the rule of data processing. This means that wrong input data or data with serious flaws will always leads to incorrect conclusions, and often, incorrect or harmful actions. In most of practical situations, it is hard to get good basic data, even in simple, non controversial situations and with the best of intentions. With the available basic data, the job of its processing, statistician needs help of various computing equipments such as computer, calculator and mathematical tables etc. Due to the limitations of computing capabilities of these equipments the calculations performed are not always accurate and are subject to some approximations. This means that howsoever fine techniques a statistician may use, if computations are inaccurate, the conclusions he draws from an analysis of numerical data will generally be wrong and very often misleading. It is essential therefore, to look into the sources of inaccuracies in numerical computations and the way to avoid them. In addition to this, before the data is actually processed, it must be ensured that the underlying assumptions for the desired analysis are satisfied because it is well known that the classical statistical techniques behave in the optimum manner under predefined set of conditions and perform badly for the practical situations where they depart significantly from the ideal described assumptions. For these situations thus there is a need to look at the data carefully before finalizing the appropriate analysis. This involves checking the quality of the data for the errors, outliers, missing observations or other peculiarities and underlying assumptions. For these rectifications, the question also arises whether the data need to be modified in any way. Further, the main purpose of classification of data and of giving graphical and diagrammatical representation is to indicate the nature of the distribution i.e. to find out the pattern or type of the distribution.   Besides the graphical and diagrammatical representation, there are certain arithmetical measures which give a more precise description of the distribution. Such measures also enable us to compare two similar distributions and are helpful for solving some of the important problems of statistical inference. 

Thus there is a need to look into these aspects i.e. inaccuracies, checking of abnormal observations, violation of underlying assumptions of data processing and summarization of data including graphical display.

The first step of data analysis is the detailed examination of the data. There are several important reasons for examining data carefully before the actual analysis is carried out. The first reason for examination of data is for the mistakes which occur at various stages right from recording to entering the data on computer. The next step is to explore the data. The technique of exploratory data analysis is very useful in getting quick information, behaviour and structure of the data. Whereas the classical statistical techniques are designated to be best when stringently assumptions hold  true. However it is seen that these techniques fail miserably in the practical situation where the data deviate from the ideal described conditions. Thus the need for examining data is to look into methods which are robust and resistant instead of just being the best in a narrowly defined situation. The aim of exploratory data analysis is to look into a procedure which is best under broad range of situations. The main purpose of exploratory data analysis is to isolate patterns and features of the data which in turn are useful for identifying suitable models for analysis. Another feature of exploratory approach is flexibility, both in tailoring the analysis to the structure of the data and in responding to patterns that successive steps of analysis uncover.

Graphical Representation of Data

The most common data structure is a collection of batch of numbers. This simple structure, in case of large number of observations, is sometimes difficult to study and scan thoroughly with just looking into it. In order to concise the data, there are number of ways by which the data can be represented graphically. The histogram is a commonly used display. The range of observed values is subdivided into equal intervals and then the cases in each interval are obtained. The length of the interval is directly proportional to the number of cases within it. A display closely related to the histogram is the stem-and-leaf plot.

Stem-and-leaf Display

The stem-and-leaf plot provides more information about the actual values than does a histogram.  As in the histogram, the length of each bar corresponds to the number of cases that fall into a particular interval. However, instead of representing all cases with a same symbol, the stem-and-leaf plot represents each case with a symbol that corresponds to the actual observed value. This is done by dividing observed values into two components - the leading digit or digits, called the stem and the trailing digit called the leaf. The main purpose of stem-and leaf display is to throw light on the following :

            (1) Whether the pattern of the observation is symmetric.

            (2) The spread or variation of observation.

            (3) Whether a few values are far away from the rest.

            (4) Points of concentration in data.

            (5) Areas of gaps in the data.

Example: For the data values 22.9, 26.3, 26.6, 26.8, 26.9, 26.9, 27.5, 27.6, 27.6, 28.0, 28.4, 28.4, 28.5, 28.8, 28.8, 29.4, 29.9, 30.0. Display stem and leaf diagram.

For the first data value of 22.9

Data value                   Split                 Stem                and                  Leaf

    22.9                         22/9                 22                                              9

Then we allocate a separate line in the display for each possible string of leading digits (the stem), the necessary lines run from 22 to 31. Finally we write down the first trailing digit (the leaf) of each data value on the line corresponding to its leading digits.

                        (Unit = 1 day )

22        :  9

23        :                      

24        :                      

25        :                      

26        :  3          6          8          9          9

27        :  5          6          6

28        :  0          4          4          5          8          8

29        :  4          9

30        :  0          3

31        :  2          8

Sometimes, there are too many leaves per line (stem) then in that case it is desired to split lines and repeat each stem.

            0          *          (Putting leaves 0 through 4)

            0          .           (Putting 5 through 9)

            1          *

            1          .

            2          *

            2          .

In such a display, the interval width is 5 times a power of 10. Again, even if for two lines it is crowded then we have a third form, five lines per stem.

            0*

            t

            f

            s

            0.

With variables 0 and 1 on the * line, 2 (two) and 3 (three) on the t line, 4 (four) and 5 (five) on the  f  line, 6 (six) and 7 (seven) on the  s  line and 8 and 9 on the  .  line.

The Box-plot

Both the histogram and the stem-and-leaf plots are useful for studying the distribution of observed values. A display that further summarizes information about the distribution of the values is the box-plot. Instead of plotting the actual values, a box plot displays summary statistics for the distribution. It plots the median, the 25th percentile, 75th percentile and values that are deviating from the rest. Fifty percent of the cases lie within the box.  The length of the box corresponds to the interquartile range, which is the difference between the Ist and 3rd quartiles. The box plot identifies extreme values which are more than 3 box-lengths from the upper or lower edge of the box. The values which are more than 1.5 box-lengths are characterized as outliers. The largest and the smallest observed values are also part of the box-plot in terms of edges of lines. The median which is a measure of location lies within the box. The length of box depicts the spread or variability of observations. If the median is not in the center of the box, the values are skewed. If the median is closer to the bottom of the box than the top, the data are positively skewed. If the median is closer to top then the data are negatively skewed.

Spread-versus-level plot

When a comparison of batches shows a systematic relationship between the average value or level of a variable and the variability or spread associated with it,  then it is of interest to search for a re-expression, or transformation of the raw data that reduces or eliminates this dependency. If such a transformation can be found, the re-expressed data will be better suited both for visual exploration and for analysis. This will further make analysis of variance techniques valid and more effective, when there is exactly or approximately equal variance across groups. The spread-versus-level plot is useful for searching an appropriate power transformation. By power transformation it is meant as power i.e. searching a power (or exponent)  p  as the transformation that replaces x by x^p . The power can be estimated from the slope of line in the plot of log of the median against the log of the interquartile range i.e. IR a M_d = c M_d or log IR = log c + B log M_d . The power is obtained by subtracting the slope from 1. (i.e. Power = 1 - slope). This is based on the concept that transformation Z =  x^1-b of the data given re-expressed value Z whose interquartile range or spread does not depend at least approximately on the level. In addition to this graphical method of  judging the independence of spread and level, there is a test known as Levene Test for testing the homogeneity of variances.

Although there is a wide variety of tests available for testing the equality of variances, but many of them are heavily dependent on the data being samples from normal populations. Analysis of variance procedures on the other hand are reasonably robust to departures from normality. The Levene test is a homogeneity of variance test that is less dependent on the assumption of normality than most tests and thus is all the more important with analysis of variance. It is obtained by computing for each case the absolute difference from its cell mean and then performing a one-way analysis of variance on these differences.

Read more

A Statistical-Why?

Q1. Why do we study samples when we want to know about populations?

Samples that representing the population are preferable because:

Cost: Cost is one of the main arguments in favor of sampling, because often a sample can furnish data of sufficient accuracy and at much lower cost than a census.

Accuracy: Much better control over data collection errors is possible with sampling than with a census, because a sample is a smaller-scale undertaking.

Timeliness: Another advantage of a sample over a census is that the sample produces information faster. This is important for timely decision making.

Amount of Information: More detailed information can be obtained from a sample survey than from a census, because it take less time, is less costly, and allows us to take more care in the data processing stage. Destructive Tests: When a test involves the destruction of an item under study, sampling must be used. Statistical sampling determination can be used to find the optimal sample size within an acceptable cost.

  

Q2. Why do we study random sample instead of just any sample?

Random sampling provides equal chance to each individual member of the population to be selected for investigation.  Random samples therefore are unbiased in their being representative of the population under investigation.

  

Q3. Why is the median sometimes better than the mean as an indicator of the central tendency?

The central tendency is often measured by the mean because the other two measures namely median and node are almost the same for a homogeneous population having symmetric distribution. However, if the distribution is severely skewed, then one must use the median as a single value representing population, such as salary in your organization.

Q4. Why is standard deviation a better measurement of data variation than the range?

Standard deviation uses the entire data, while the range uses only the two extreme values.  Therefore, range is sensitive not only to the outliers but less stable than standard deviation.

Q5. Why is P(A and B) = P(A)P(B|A) = P(B)P(A|B)?

 It is by definition that P(A|B) = P(A and B)/P(B) provided P(B) is non-zero.

Similarly, P(B|A) = P(A and B)/P(A) provided P(A) is non-zero.

The rest follows. Right?

Q6. Why is P(A or B or both) = P(A) + P(B) – P(AÇB)?

 P(A or B or both) = P(only A) + P(only B) + P(both) = 

 [P(A) - P(both)] + [P(B) -  P(both)] + P(both) =

 P(A) + P(B) - P(both) = P(A) + P(B) – P(AÇB

Right?

Q7. If in an experiment there are three possible outcomes (a, b, c) and their probabilities are P(a) = .3, P(b) = .4, and P(c) = .5, why must at least two of the three outcomes not independent of each other?

 Since the sum of the probabilities is not equal to one, it implies that these three events are not Simple Events.  That is, at least one of the events is a composite event depending on at least one of the other events. 

  

Q8. Why do we use S(x – x _bar)² to measure variability instead of S(x - x_bar)?

Because, if we add up all positive and negative deviations, we get always zero value, i.e., S(x – x _bar) = 0. So, to deal with this problem, we square the deviations. Why not using power of four (three will not work)? Squaring does the trick; why should we make life more complicated than it is?

Notice also that squaring also magnifies the deviations; therefore it works to our advantage to measure the quality of the data.

  

Q9. To approximate the binomial distribution, why do we sometimes use the Poisson distribution and sometimes use the normal distribution?

Poisson approximation to binomial is a discrete-to-discrete approximation; therefore it is preferable to the normal approximation.  However, just as binomial table is limited, the Poisson table is limited too in its scope; therefore one may have to approximate both by normal.

Q10. Why is the (1 – a)100% confidence interval equal to x ± z_a/2s_x?

It is the case of Single Observation, i.e., n=1. Therefore, if the population is normal with known standard deviation s_x then the above confidence interval is correct.

  

Q11. Why are stratified random samples “random”?

Whenever we have a mixture of population, no standard statistical technique is applicable.  In such a case one must take sample from each stratum randomly and then apply statistical tools to each sub-population.  Never mix apples with oranges.

Q12. Why are cluster samples “random”?

It is similar to the stratified sampling in its intents, however often cluster sample are within each cluster randomly.

Q13. Why do we usually test for Type I error instead of Type II error in hypothesis testing?

Because the null hypothesis is always specified in exact form with (=) sign.  Therefore one can talk about rejecting or not rejecting the null hypothesis.  However, if the alternative is also specified in exact form with (=) sign, then one in able to compute both types of errors.

Q14. Why the “margin of error” is often used as a measure of accuracy in estimation?

When estimating a parameter of a population based on a random sample, one has to provide the degree of accuracy.  The accuracy of the estimate is often expressed by a confidence interval with specific confidence level. 

The half-length of the confidence interval is often referred to as absolute error, absolute precision, and even margin of error.  However, the usual usage of the “marginal of error” is referred to the half-length of confidence interval with 95% confidence.

 

Q15. Why there are so many statistical tables? Which one to use?

Statistical tables are used to construct confidence interval in estimation, as well as reaching reasonable conclusions in test of hypotheses.  Depending on application areas, one may, for example classify the two major statistical tables as follows:

T - Table: expected value of population(s), regression coefficients, and correlation(s).

Z - Table: Similar to the T-table, with large-size (say over 30).

Q16.  Why do we use the p-value? What is it?

The p-value is the tail probability of the test statistic value given that the null hypothesis is true. Since the p-value is a function of a test statistic, which is a function of sample data, therefore it is a statistic as well as a conditional probability.This is analogous to the method of maximum likelihood parameter estimation wherein we consider the data to be fixed and the parameter to be variable.

Q17. Why is linear regression a good model when the range of the independent variable is small?

Most statistical models are not linear, however if we are interested in a small range then, almost all non-linear function can be approximated by a straight line.

Q18. Why does high correlation not imply causality?

Determination of cause-and-effect is not in the statistician’s job description.

Any specific cause-and –effect belongs to specific areas of knowledge subject to rigorous experimentation. Correlation measures the strength of linear numerical relation, called function.  A function simply converts something into something else.    Your coffee grounder is a function.  The cause in this example is mechanical force in grounding the coffee bins.     

Q19. Why would ANOVA and performing t-test for each pair of samples not necessarily give the same conclusion at the same confidence level?

It is because any pair-wise comparison of means is never a substitute for the simultaneous comparison of all means. Moreover, it is not an easy task to compute the exact confidence level from the pair-wise confidence levels.

Read more

Statistics behind A/B Testing

A/B testing is one of the primary tools in any data-driven environment. A/B Testing lets you compare several alternate versions of the same reality simultaneously and see which produces the best outcome.

It’s basically testing the effectiveness of different designs to find the optimum solution. These tests are usually performed on live realities with real users who are completely unaware of the test. A/B Testing is a way of conducting an experiment where you compare a control group to the performance of one or more test groups by randomly assigning each group a specific single-variable treatment

Why not test A for a while then B?

Just look at any graph of your outcome over time. Some months can be 30% better than the previous month, then it gets worse again, then better, and so on…outcome are affected by season of the year, sources of users, news events, the state of the economy, competitor activity… You’ll see big differences and big swings even with no changes at all. So if you tried A in a good month then tried B in a bad month you could make an incorrect decision. You’re testing the two versions at the same time in the same season with similar users. It does not have to be 50/50. It could be 90 / 10 or any other ratio.

Building Treatments

Once you know what you want to test you have to create treatments to test it. One of the treatments will be the control. The other treatments will be variations on that. Foe example here are some things worth testing on a website:

•    Layout - Move the registration forms around. Add fields, remove fields.

•    Headings - Add headings. Make them different colors. Change the copy.

•    Copy - Change the size, color, placement, and content of any text you have on the page.

You can have as many treatments as you want, but you get better data more quickly with fewer treatments.

Randomization

You can’t just throw up one test on Friday and another test on Saturday and compare
— there’s no reason to believe that the outcome for users on a Friday is the same for users on a Saturday. To be valid, trials need to be sufficiently large. By tossing a coin 100 or 1000 times one reduce the influence of chance, but even then  gets slightly different results with each trial. Similarly, a test may have 30% outcome on Monday, 35% on Tuesday and 28% on Wednesday. This random variation should always be the first cause considered of any change in observed results.

A/B testing solves this by running the experiment in parallel and randomly assigning a treatment each person who visits. This controls for any time-sensitive variables and distributes the population proportionally across the treatments.

Maximizing your outcome is not simply a matter of making changes, it's about making the right changes,at the right time, in the right sequence, and then evaluating the outcomes before continuing the process.

You divide your audience into two groups. You expose one group to the original version of whatever you are testing. You expose the other group to an alternative version, in which only one element has been changed. Then you track the outcomes.

Here are some possibilities to get you started:

Emails: bonus gifts, coupons, messages, guarantees, opening sentence image, closing sentence image, from-field, calls to action, opening greetings, type styles, layout elements, graphic images, etc.

Web Sites: landing pages, language of copy (headings, body, calls to action, assurances), colors, location of elements, look/feel, hyperlinks, etc.

Statistical hypothesis

How hypothesis testing can tell you whether your A/B tests actually effect user behavior, or whether the variations you see are due to random chance. Hypothesis testing is all about quantifying our confidence, so let’s get to it.
Statisticians use something called a null hypothesis to account for this possibility. The null hypothesis for the A/B test might be something like this:

- The difference in conversion between Version A and Version B is caused by random variation. It’s then the job of the trial to disprove the null hypothesis. If it does, we can adopt the alternative explanation:
- The difference in conversion between Version A and Version B is caused by the design differences between the two.

To determine whether we can reject the null hypothesis, we use certain statistical equations to calculate the likelihood that the observed variation could be caused by chance, which include Student’s t test, χ-squared and ANOVA.
Statistical significance

If the arithmetic shows that the likelihood of the result being random is very small (usually below 5%), we reject the null hypothesis. In effect we’re saying “it’s very unlikely that this result is down to chance. Instead, it’s probably caused by the change we introduced” – in which case we say the results are statistically significant.

The Statistics

We need to start with a null hypothesis. In our case, the null hypothesis will be that the outcome of the control treatment is no less than the outcome of our experimental treatment. Mathematically

where pc is the conversion rate of the control and p is the outcome of one of our experiments. The alternative hypothesis is therefore that the experimental object has a higher outcome. This is what we want to see and quantify. The sampled conversion rates are all normally distributed random variables. We have “converts” or “doesn’t convert.” Instead of seeing whether it deviates too far from a fixed percentage we want to measure whether it deviates too far from the control treatment.
Here’s an example representation of the distribution of the control outcome and the treatment outcome.

The peak of each curve is the outcome we measure, but there’s some chance it is actually somewhere else on the curve. Moreover, what we’re really interested in is the difference between the two outcomes. If the difference is large enough we conclude that the treatment really did alter user behavior. So, let’s define a new random variable

 

then our null hypothesis becomes

 

 Using the random variable X, we need to know the probability distribution of X.

Z-scores and One-tailed Tests
Mathematically the z-score for X is

where N is the sample size of the experimental treatment and Nc is the samle size of the control treatment because the mean of X is p – pc and the variance is the sum of the variances of p and pc.

In this case our null hypothesis is

In other words, we only care about the positive tail of the normal distribution. In this example we only reject the null hypothesis if the experimental outcome is significantly higher than the control outcome, so we have 

That is, we can reject the null hypothesis with 95% confidence if the z-score is higher than the tabulated value.

Read more

Statistical Concepts For Life

Statistics provides justifiable answers to the following concerns for every consumer and producer: 

- What is your or your customer's, Expectation of the product/service you sell or that your customer buys? That is, what is a good estimate for µ? 

- Given the information about your or your customer's, expectation, what is the Quality of the Product/service you sell or that your customers buy from your products or services? That is, what is a good estimate for quality (e.g., σ, or C.V.)? 

 - Given the information about your or your customer's expectation, and the quality of the Product/service you sell or you customer buy, how does the product/service compare with other existing similar types? That is, comparing several µ's, and several σ's.

1.  Statistical techniques are methods that convert data into information. Descriptive techniques describe and summarize; inferential techniques allow us to make estimates and draw conclusions about populations from samples.

2.  We need a large number of techniques because there are numerous objectives and types of data. There are three types of data: quantitative (real numbers), qualitative (categories) and ranked (rating). Each combination of data type and objective requires specific techniques.

3.  We gather data by various sampling plans. However, the validity of any statistical outcome is dependent on the validity of the sampling.

4.  The sampling distribution is the source of statistical inference. The interval estimator and the test statistic are derived directly from the sampling distribution.

5.  All inferences are actually probability statements based on the sampling distribution. Because the probability of an event is defined as the proportion of times the event occurs in the long run, we must interpret confidence interval estimates in these terms.

6.  All tests of hypotheses are conducted similarly. We assume that the null hypothesis. We than compute the value of the test statistic. If the difference between what we have observed (and calculate) and what we expect to observe is too large, we reject the null hypothesis. The standard that decides what is "to large" is determined by the probability of a Type I error. 

7.  In any test of hypothesis (and in most decisions) there are two possible errors, Type I and Type II errors. The relationship between the probabilities of these errors helps us decide where to set the standard. If we set the standard so high that the probability of a Type I error is very small, we increase the probability of a Type II error. A procedure designed to decrease the probability of a Type II error must have a relatively large probability of a Type I error.

8.  The sampling distributions that are used for quantitative data are the Student-t, chi-square statistic and the F.  We can use the analysis of variance in place of the t-test of two means. We can use regression analysis with indicator variables in place of the analysis of variance. We often build a model to represent relationships among quantitative variables, including indicator variables.

9.  When you take a sample from a population and compute the sample mean, it will not be identical to the mean you would have gotten if you had observed the entire population.  Different samples result in different means. The distribution of all possible means values of the mean, for sample of a particular size, is called the sampling distribution mean.

10.  The variability of the distribution of sample means depends on how large your sample is and on how much variability there is in the population from which the samples are taken. As the size of the sample increases, the variability of the sample means decreases. As variability in a population increases, so does the variability of the sample means.

11.  A normal distribution is bell-shaped. It is a symmetric distribution in which the mean, median, and mode all coincide. In the population, many variables, such as height and weight, have distributions that are approximately normal. Although normal distributions can have different means and variances, the distribution of the cases about the mean is always the same. You use standard Z scores to locate an observation within a distribution. The mean of standard Z scores is 0, and the standard deviation is 1.

12.  The Central Limit Theorem states that for samples of a sufficiently large size, the distribution of sample means is approximately normal.  (That's why the normal distribution is so important for data analysis.)

13.  A confidence interval provides a range of values that, with a designated likelihood, contains e.g. the population mean, or σ.

14.  To test the null hypothesis that two population mean are equal, you must calculate the probability of seeing a difference at least as large as the one you've observed in your two samples, if there is no difference in the populations.

15.  The probability of seeing a difference at least as large as the one you've observed, when the null hypothesis is true, is called the observed significance level, or P-value.  If the observed significance level is small, usually less than .05, you reject the null hypothesis.

16.  If you reject the null hypothesis when it's true, you make a Type 1 error. If you don't reject the null hypothesis when it's false, you make a Type 2 error. 

17. The techniques used on qualitative data require that we count the number of times each category occurs (e.g., the Runs test). The count is then used to compute statistics. The sampling distributions we use for qualitative data are the Z (i.e., the standard normal) and the chi-squared distributions.

18.  The techniques used on ranked data are based on a ranking procedure. Statisticians call these techniques nonparametric. Because the requirements for the use of nonparametric techniques are less than those requirements for a parametric procedure, we often use nonparametric techniques in place of parametric ones when any of the required conditions for the parametric tests is not satisfied. 

19.  We can obtain data through experimentation or by observation. Observational data lend themselves to several conflicting interpretations. Data gathered by an experiment are more likely to lead to a definitive interpretation.

20.  Statistical skills enables to intelligently collect, analyze and interpret data relevant to their decision-making. Statistical concepts and statistical thinking enables to: Solve problems in a diversity of contexts, Add substance to decisions, Reduce guesswork.

Read more

Examination of Normality

Most of the parametric tests follow the assumption of normality. Normality means that the distribution of the test is normally distributed with 0 mean, with 1 standard deviation and a symmetric bell shaped curve. As the normal distribution is very important for statistical inference point of view so it is desired to examine the assumption to test whether the data is from a normal distribution. You can use a statistical test and or statistical plots to check the sample distribution is normal.
The normality can be tested by plotting a normal plot. In a normal probability plot each observed value is paired with its expected value from the normal distribution. In a situation of normality, it is expected that points will fall on straight line. In addition to this a plot of deviation from straight line can also be plotted as detrended normal plot. A structure-less detrended normal plot confirms normality. 

Histogram: Histogram gives the rough idea of whether or not data follows the assumption of normality.

Q-Q plot: Most researchers use Q-Q plot to test the assumption of normality. In this method, observed value and expected value are plotted on a graph. If the value varies more from a straight line, then the data is not normally distributed. Otherwise data will be normally distributed.

Box plot: Box plot test is used to test if there are outliers present in the data. Outliers and skewness show the violation of the assumption of normality.

Besides these visual displays, the statistical tests are Shappiro-Wilks and the Lilliefors. The Lilliefors test is based on the modification of the Kolmogorov-Smirov test for the situation when means and variances are not known but are estimated from the data. The Shapiro-Wilks test is more powerful in many situations as compared to other tests.

•  Kolmogorov-Smirnov test

Test based on the largest vertical distance between the normal cumulative distribution function (CDF) and the sample cumulative frequency distribution (commonly called the ECDF – empirical cumulative distribution function). It has poor power to detect non-normality compared to the tests below.
•  Anderson-Darling test

Test similar to the Kolmogorov-Smirnov test, except it uses the sum of the weighted squared vertical distances between the normal cumulative distribution function and the sample cumulative frequency distribution. More weight is applied at the tails, so the test is better able to detect non-normality in the tails of the distribution. 

•  Shapiro-Wilk test 

A regression-type test that uses the correlation of sample order statistics (the sample values arranged in ascending order) with those of a normal distribution.

How to interpret the normality test 

For each test, the null hypothesis states the sample has a normal distribution, against alternative hypothesis that it is non-normal. The p-value tells you the probability of incorrectly rejecting the null hypothesis. When it’s significant (usually when less-than 0.10 or less than 0.05) you should reject the null hypothesis and conclude the sample is not normally distributed. When it is not significant (greater-than 0.10 or 0.05), there isn’t enough evidence to reject the null hypothesis and you can only assume the sample is normally distributed. However, as noted above, you should always double-check the distribution is normal using the Normal Q-Q plot and Frequency histogram.

Read more

Recency Frequency Monetary Modeling (RFM)

RFM analysis is a technique used to group or segment existing customers based on historic behavior in the hopes that history can, with the right motivators, be caused to repeat or even improve upon its self. The acronym is short for Recency, Frequency and Monetary value and each of these measures aligns to one or more of the three methods of increasing revenue for a business.

RFM is an effective process for marketing to your loyal customers and uses purchase behavior by recency, frequency and monetary to determine what offers work for what type of customers. Generally, only small percentages of customers respond to typical offers. But with RFM, you can ensure you are targeting the right set of customers who are most likely to respond. RFM is a powerful segmentation method for predicting customer response and ensures improvement in response as well as profits.

It is used primarily for targeted campaigning, customer acquisition, cross-sell, up-sell, retention, etc and is a guarantor of campaign effectiveness and optimization.

One of the most commonly used forms of segmentation is RFM (recency, frequency and monetary value). RFM is a good way to define and understand customer value. As well as helping customer development it can also form the basis of a good customer retention strategy.

Defining the Terms of RFM

Just what are “recency,” “frequency,” and “monetary” measures? The concepts are simple, even intuitive but turning them into measures that you can use to produce RFM scores can be somewhat tricky.

Keep in mind that the measures you use to rank your list are not the same numbers as the 5-4-3-2-1 score that you assign to each customer. For recency, you’ll figure out how long it’s been since each customer interacted, in days, weeks, or months. You then use those time-based measures to rank your list in order, from most recent to the long-lapsed. The recency score comes from that ranked list, with the 20 percent who gave most recently assigned a score of 5.For frequency, the measure is number of interactions in a given period. For monetary, the measure is total transaction value.

-Recency

When did the customer last place an order, visit our store or interact with us in a material way? A customer who recently had a favorable interaction with our firm is, we hope, predisposed to repeating that interaction and thus susceptible to an offer that would encourage future business. Similarly a customer who hasn’t done business with us for sometime may be open to an offer of resumption that draws them back.

-Frequency

How many interactions, over a period of time, has the customer had with us? Assuming the interactions have been favorable for both parties, we would hope that we can sustain or increase the frequency of the interactions to our advantage. As with a customer who has not done business with us recently, frequency of interaction is a trigger you will want to pay attention to when it falls off over a period of time. This is where the frequency measure is often correlated to the recency one.

-Monetary

Over a given period of time, or number of interactions, what is the value of the customers business either in terms of revenue or profitability? Grouped in with monetary analysis is often inventory and channel analysis to get a sense of customers whose purchases reflect higher margin activities for the business such as buying large volumes through automated channels or the purchase of inventory items that have higher margins, are slow moving in various periods or are ends or remnants of other jobs.

Why does my business need RFM?

RFM will be of benefit to your business in any number of ways. If your business is wasting money speaking to customers who are of little worth to you, or may have even ceased being a customer, then RFM segmentation can help. The Recency segment tells you which customers have ceased trading with you, and the monetary segments tell you who your real big hitters are. Let’s suppose that your marketing budget is slashed next year by half. Who are you going to spend that money on talking to? RFM allows you to segment your customer base in a way that empowers your business to spend that budget in the right way, on the right customers. Single purchasers make up a large portion of most customer bases. Businesses buy from you, and then you never see them again. If you are trying to identify and get these businesses to repeat purchase, then RFM segmentation is for you. Regular RFM reporting will give you visibility on who your newest customers are. You can then market to them to try and get that repeat purchase.

Some examples:

i) Catalog and direct-mail marketers were early adopters of RFM techniques to determine which customers got which catalogs, how often and with what special incentives, coupons or savings. With the advent of high capacity colour digital presses, many companies now custom print each catalog, varying the items on pages, prices for items and even specialized promotional offers for each customer based on the findings of RFM analysis.

ii) RFM analysis forms the basis of every customer loyalty program in operation from frequent flyer or hotel guest programs to retail shopper reward cards.

iii) If you’ve ever been to a casino you’ve seen RFM analysis combined with life-time value analysis. These are the principles upon which casinos issues complementary hotel rooms, meals, show tickets and everything else they offer “for free” to patrons of their establishments. Even the so called “free drinks” you can get in a casino are carefully distributed based on a real time size-up of your value to the casino based on RFM analysis.

Read more